Teaching Basic Addition...
Before getting into matters as they relate to teaching basic addition, I feel it is important for all parents to read the section I wrote on "short term memory" issues in my Updates section in order to understand issues I feel are critical to teaching certain skills. It is important, in my opinion, that you also read the section under Parent Observations that relates to the topic of short term memory also. In this discussion, I discuss how I started to teach Zachary basic math... based on a set of very specific flash cards I made for him. These flashcards are described in the "short term memory" section under Parent Observations. Anyone can make these flashcards for about $1.00.
As I worked with the flashcards I had made for Zachary, I found he was very enthusiastic about going through them. Whenever I saw Zachary hesitating in the least, before he would "guess" and give a "bad answer" I always made sure he could look at the correct answer. In my opinion, a bad guess is still an "utterance" and I don't want a "bad guess" to be confused down the road with the correct answer. Thus, if Zachary does not know the answer, I always provide it quickly for him, make him repeat it, and then go on.
What I did find in working with the flashcards, however, was that for the larger numbers, Zachary often hesitated. In my opinion, this was due to 2 things... the fact that he obviously did not know the answer... but, also, at times, he seemed a little confused that more than one "combination" of numbers could add up to the same thing something else added up to. For example, he quickly grasped the 2+2 = 4, 5+5=10, etc.... but, he would hesitate on 4+6=10 or 3+7=10 or 2+8=10. It then occurred to me that just as in teaching colors, if "blue" is said to be "blue" then to introduce "another blue" was confusing... likewise, I think the same thing applies here... that 5+5=10 and to introduce "other 10s" was confusing Zachary. What I did find useful for Zachary was to use the "same number additions" (i.e., 2+2 = 4, 3+3 = 6, 4+4 = 8, etc.) as "PEGS" or reference points. So, when teaching 5+6 for example, I'd remind Zachary that if "5+5 = 10, then, 5+6 = ?" and he could usually give me the answer because he had figured out the "add 1 more" concept.
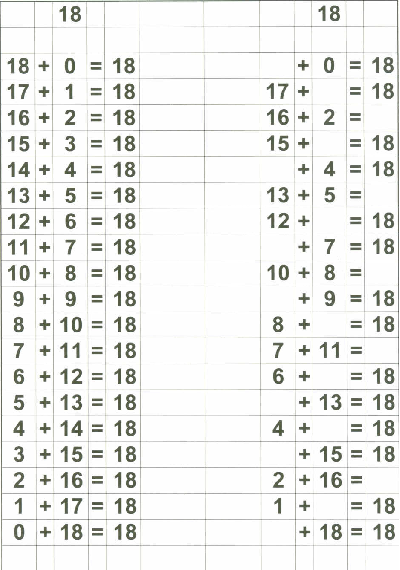
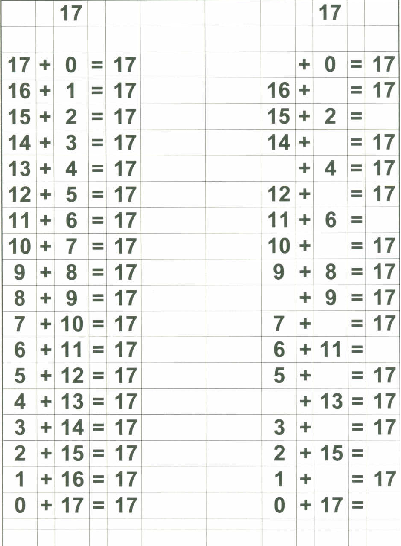
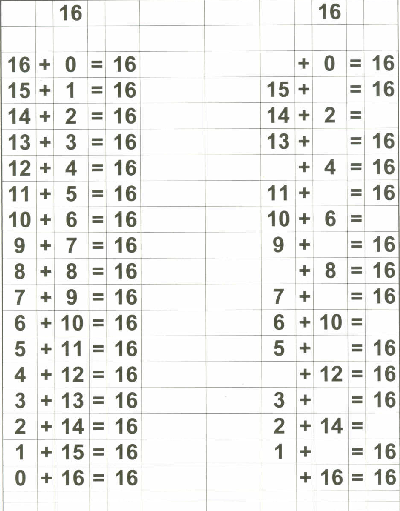
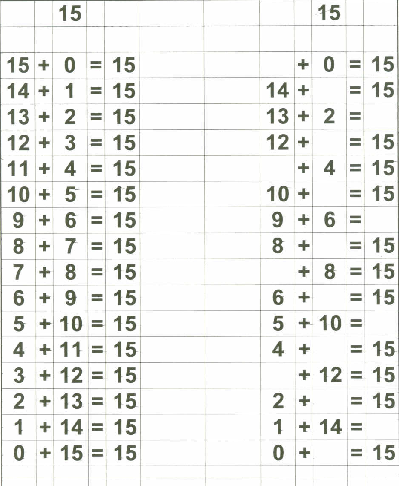
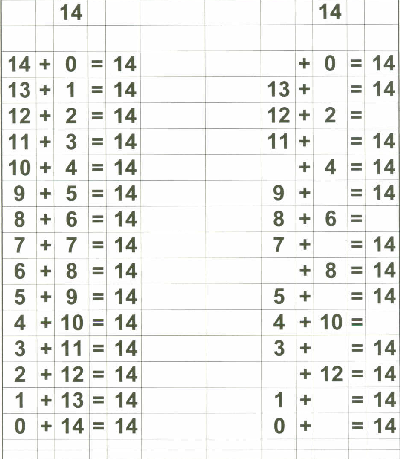
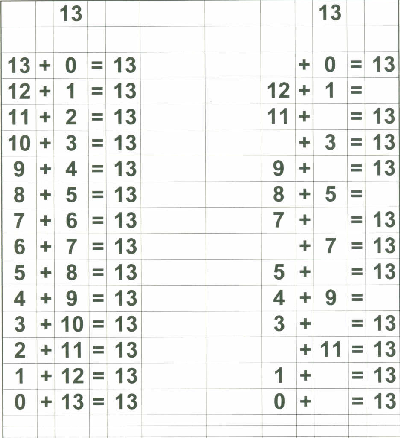
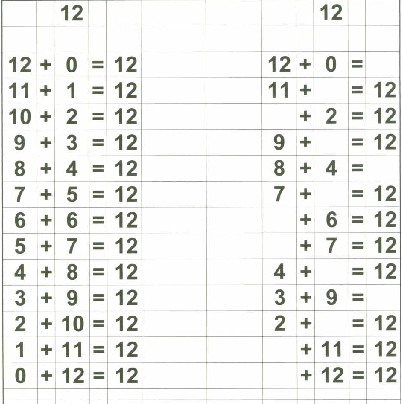
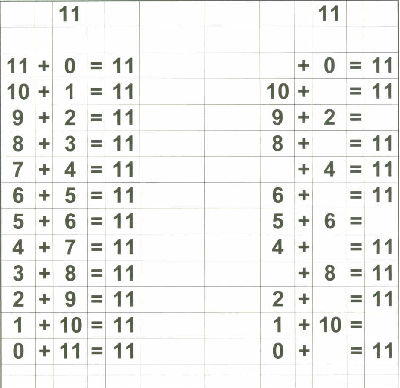
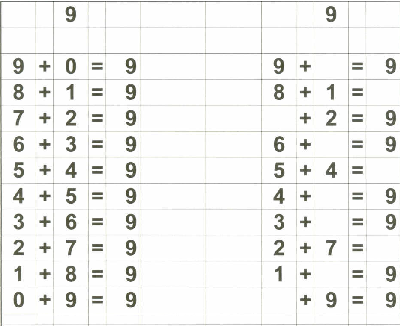
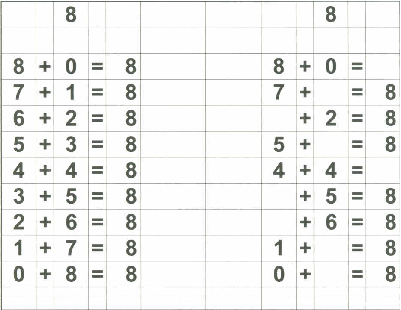
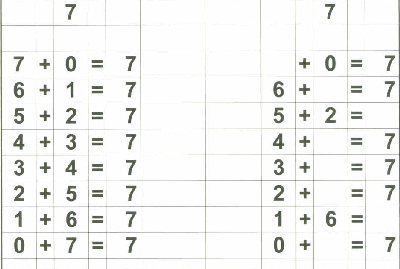
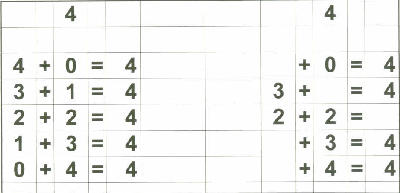
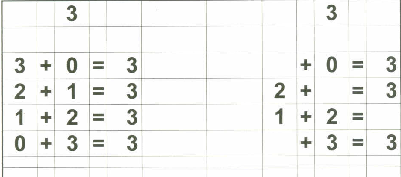
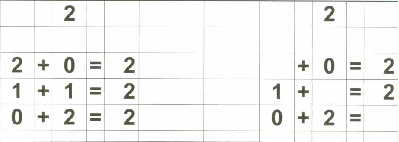
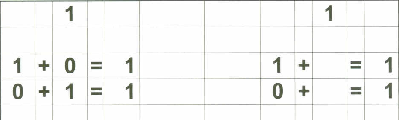
Therefore, in addition to my flashcards (which I still plan on using), I decided to make up "reference cards" for Zachary... to show him all the possible combinations of numbers that add up to 0 through 18. I stopped at 18 because I then plan on teaching the concept of "carry the one" and 9+9=18 is the "highest" number he needs to know before going on to "carry the one" type operations.
Below are examples of the 18 "reference cards" I made for Zachary. I made them in such a way that if I wanted to, I could fold the page in half to provide the "reference" on one side and the "practice" on the other side if I chose to do that.
Of course, Zachary understands the basic concept of "addition" since we started practicing that on fingers a long time ago. That, in my opinion, is the best place to start with a child in teaching basic addition. What follows is the "next step" - getting to memorization of basic addition through 18.
After these reference cards are mastered, I plan on teaching Zachary the concept of "carry the one". I provide an example of how I plan on doing that at the very bottom of this section. I will then use similar methods for subtraction... I'm just not up to that yet and need to do a little more thinking on how I best want to teach subtraction to Zachary. We are already doing subtraction "on fingers" but, obviously, the next step for that will have to follow soon too. :o)
Again, I caution all parents who want to try this not to get "over ambitious". I find it is best to teach a little each day rather than get over ambitious and have Zachary get confused because I'm introducing "too much" at once. These are copyrighted materials, but, "same rules" apply for those to whom I grant permission to use these materials free of charge. :o)




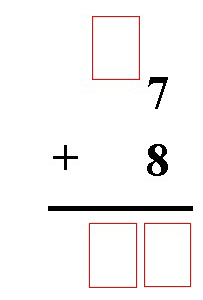
Teaching The Concept Of “Carry The One" Or More Accurately.. "Carry The Number”
I have not started to teach this yet, but when I do, this is what I plan on doing. Since I know Zachary loves puzzles, I plan on using that to my advantage to make math "look more" like a puzzle to be solved by adding "boxes" that he will need to "fill in". I'm hoping that will work better than just saying "carry the one", because the "one" may actually be a bigger number and I don't want to confuse him by making him think it might only be a "1" that goes into the box. So, I'll also be careful to say that this is called, "carry the number". The other thing I'm considering doing is "adding the boxes" to the flashcards I have already made (described under the short term memory section in Parent Observations) so that they look like what is shown below. I'll have to add the boxes for both sides of the flashcard. :o)
I'm still thinking about the best way to teach subtraction, but, I'm sure it will be something very similar to what I have for addition. Again, these are just "my best guess" as to what I think will work for Zachary. If it works for others - great! :o)